什么導(dǎo)致了成功,當(dāng)然有很多因素。有的人勤奮,有的人幸運,有的人有貴人的幫助等等。但什么導(dǎo)致了失敗,原因也是很多的。但這里我只講三個容易導(dǎo)致我們失敗的原因,看了你一定會有收獲。
第一個原因:莫名其妙地湊熱鬧。假設(shè)你現(xiàn)在走在去圖書館的路上,打算去看一天復(fù)習(xí)資料。突然看到路邊一堆人聚集在一起,不知道看什么。你也上去圍觀,看了一會兒,才去圖書館學(xué)習(xí),結(jié)果浪費了學(xué)習(xí)的時間。在學(xué)習(xí)的過程中,心中還老想著剛才發(fā)生的事兒,導(dǎo)致自己的復(fù)習(xí)效果也很差。其實,既然是路邊的熱鬧,那就一定是與你無關(guān)的啊!再說路邊能發(fā)生啥事?無非就是倆人吵架了之類的,跟你有什么關(guān)系啊?把這些時間用來學(xué)習(xí),提高一兩分不好么?
第二個原因:心急火燎地隨大流。有些同學(xué)看到身邊的人都去聽了這個課程,買了那本資料,抄了幾個模板。于是跟風(fēng)效仿,也開始東一榔頭西一棒槌的跟風(fēng)。最終的結(jié)果,就是自己欠缺的地方,一點都沒補上來,跟風(fēng)學(xué)習(xí)的內(nèi)容,最后也證明沒多大用處。何必呢,老老實實的把自己的基礎(chǔ)打扎實,把自己的漏洞補上去才是正道啊!
第三個原因:操碎了別人的心肝。我們有些同學(xué)是追星一族。啊!今天偶像受傷了!咦!明星又出緋聞了!哎呦!這個誰誰誰又獲獎了!我只想說,跟你有啥關(guān)系啊,天天為偶像操碎了心,自己的學(xué)習(xí)也沒學(xué)好,還不如把這閑工夫用來孝敬爹媽呢?你說對不?
1
概率題中,經(jīng)常會看到這類題:題中有“至多”、“至少”的字眼。這類題很多學(xué)生容易讀錯題意,或者是在分類計算的時候,分錯類,或者重復(fù)分類,或者有遺漏。今天我們就來做幾道這樣的題,希望能徹底掌握這類題的做法。看題:
一盒中裝有20個大小相同的小球,其中紅球10個,白球6個,黃球4個。某人隨手拿出4個,則至少有3個紅球的概率為
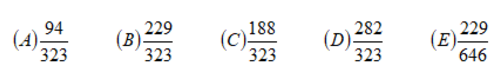
隨手抓出4個球,至少有3個紅球,那是什么意思?就是最少3個紅球唄,最少3個,那就還可以再多一些,由于只抓出來4個,所以紅球還可以是4個。所以這道題分成兩類情況:第一類,4個球中,有3個紅球,1個其他顏色的球。第二類,4個球中,4個都是紅球。
首先來算分母,總共是20個球,從中間抓4個,那這就是分母了:
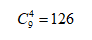
然后第一類,4個球中有3個紅球,那就是從總共10個紅球中,抓出3個紅球。剩余的一個其他顏色的球呢?從剩余的10個球中抓取。所以第一類的情況是:
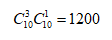
第二類呢,4個球中,全部都是紅球,那就是從總共10個紅球中,抓出4個紅球。所以第二類的情況是:
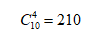
所以這道題:抓出4個球,至少3個紅球的概率是:
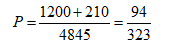
2
這是我們從正面來分析解答的一道題,有的時候,你正面去做,反而不太容易做出來,或者說,沒有反面考慮那么簡單。那我們來一道題瞧瞧:
某班有兩個課外活動小組,其中第一小組有足球票6張,排球票4張。第二小組有足球票4張,排球票6張。甲從第一小組的10張票中任抽1張,乙從第二小組的10張票中任抽1張。則兩人中至少有1人抽到足球票的概率是多少?
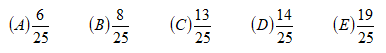
這道題是甲乙手里各有1張票,問甲乙兩人至少有1人抽到足球票的概率。那我們把問題分成三類。第一類,甲手里足球票,乙手里排球票。第二類,甲手里排球票,乙手里足球票。第三類,甲乙手里都是足球票。那如果人數(shù)再多一些,我們的分類就會更多,這時候有沒有簡單的方法來計算呢?
有的!我們的方法就是:正難則反。意思就是,正面去做搞不定,那就從反面來搞定它。
這道題說甲乙兩人至少有1人有足球票,那反過來是啥?反過來就是誰手里都沒有足球票啊!都沒有足球票,那就是甲乙手里都是排球票。而且,你發(fā)現(xiàn)沒有?反面的情況就這一種哎,很好計算哎!
那甲抽中排球的概率是:
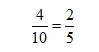
那乙抽中排球的概率是:
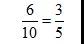
那甲乙同時抽中排球的概率是:
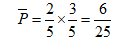
那它的反面,就是我們要求的概率,就用全部的概率(也就是1)減去這個概率,即:
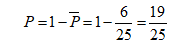
你看,有時候反其道而行之,反而是最有效的方法。
3
上面兩個講的都是“至少”的問題,下面我們來個“至多”的問題來分析分析。看題:
一批產(chǎn)品中共10件,其中有2件次品,現(xiàn)隨機地抽取5件,則5件中至多有1件次品的概率為
5件產(chǎn)品中,至多1件次品啥意思?那就是最多有1件次品。它分為兩種情況,第一類,4件正品,1件次品。第二類,5件正品,0件次品。
先求分母,分母就是10件產(chǎn)品,隨機抽取5件,那就是:
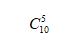
對于第一類,4件正品是從8件正品中抽取出來。1件次品是從2件次品中抽取出來。那就是:
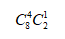
對于第二類,5件正品全部是從8件正品中抽取出來。那就是:
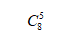
因此,概率就是:
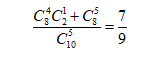
這道題我們是從正面來做的,反面當(dāng)然也可以做,不過反面沒有正面簡單而已。其實這道題如果改成:一批產(chǎn)品中共10件,其中有5件次品,現(xiàn)隨機地抽取5件,則5件中至多4件次品的概率為()。這時候我們就可以用反面來做了,你來做做試試?
好,今天的內(nèi)容我們就講解到這里。歡迎大家關(guān)注我們的公眾號,我們會持續(xù)分享院校信息、課程的推送、各科目的復(fù)習(xí)知識等內(nèi)容,一定對您的考研有很大幫助。您的關(guān)注,是我們持續(xù)的動力。我們下期再見!




