研線小課堂又開課了!一起來看看本期研線小課堂給大家帶來的干貨吧!
只要有心,生活中處處都可以發現哲理。這幾天,老師在家里陪父母看《鄉村愛情12》,頗有感悟。劇中,王木生參與賭石,花了5萬買了一塊石頭,切開后是塊好玉,當場被人50萬買走。回去后,王木生就各種場合吹噓自己眼光好、有天賦,自封玉石大師、極具天賦的投資家。
賭石和買彩票是一樣的,買的就是一個概率(相信概率學的好的同學,不會去賭博和買彩票),運氣好,說不定能發點小財,運氣不好,那這錢也就是白扔進去了。這里面,中獎還是不中,運氣的成本占99.9999%,個人能力基本上沒有。
王木生賺的這50萬里,基本上都是靠自己的運氣賺的,能力的成分基本沒有。所以,一筆生意賺了,如果運氣成分占比要大于能力成分,那就趕緊收手吧。踏踏實實的打磨好自己的能力才是正道,把希望壓在運氣上,在關鍵時刻,運氣一定離你遠去!
數學學習過程中,來不得半點虛假。會就能做對,不會就做不對。有些同學去琢磨選項的技巧,琢磨速成的方法,這些都是在把自己一年的精力、時間和金錢,押注在虛無縹緲的運氣上,最后考試怎么能考得好呢?謹記謹記!
Part.1
實數運算是我們學習的第一章,也是比較簡單的一章,因為運算對于大部分學生來說,還是比較熟悉的,最大的差別就是你運算的快一些,他運算的慢一些而已。但其中還是有一些偏難點的計算題的,比如下面這道:
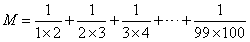
這類題一看,就不是讓我們一步步老老實實地去算答案的,不然你算一天都不一定算出來。這種類型的題,類似于小學生學的奧數內容,樣子看起來嚇人,但有固定的套路,掌握了套路,問題就能迎刃而解。
觀察一下,分母都是相鄰的兩個數相乘,而且,前一個分數分母中,相乘的兩個數中最大的那個,是下一個分數分母中,相乘的兩個數中最小的那個,依次往后排列。
這道題的解題方法就是直接將分數拆開,拆成兩個分數相減的形式,例如:
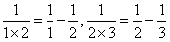
拆開以后,形狀變了,但數值不變。因此,我們把所有的分數都拆開:
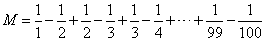
拆開以后,式子比原來長了兩倍,但仔細觀察我們發現:中間項,都可以消掉!就剩下首項和末項,因此,M的值就好算了。
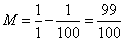
Part.2
上面是最簡單的形式,我們來看稍微復雜點的:
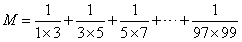
這道題每個分數中,分母是兩個相差為2的數相乘,其他規律不變。那這個能不能按照上面的那道題的解法來做呢?我們來試試,首先我們先拆開一下試試:
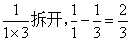
拆開后,發現數值大小發生了變化,變大了2倍,那我們可以乘以二分之一就可以了,我們拆開其他的試試看:
發現也是一樣的增大了2倍,后面的都是拆開后,增大了2倍,要想保持數值不變,我們就在拆開后的整個式子的外面,乘上一個二分之一:
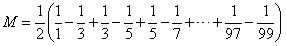
然后消掉中間項,答案就出來了:
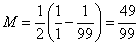
上面兩道題,分母位置上相乘的兩個數,相差分別是1和2。我們擴大一下相乘的兩個數的差距,來看看是什么情況,例如:
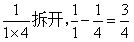
拆開后的結果比原數值增大了3倍,這個3正好就是分母位置上相乘的兩個數相差的數值。由此,我們可以得出這類題的解法了:
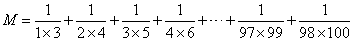
相差幾,提出幾分之一,然后直接裂項。
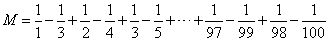
這就是我們說的,裂項相消法的做法。
Part.3
當然了,我們不會簡單的就講到這里,下面我們再增加一點難度,看你會不會跳進老師挖的坑里:
這道題和上面的那道題有些微的區別,我們做做看,首先還是:相差幾,提出幾分之一,然后直接裂項:
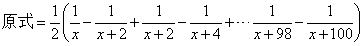
然后我們開始消除中間的項。這里要注意了,消除中間項的時候,一定要看清楚,有些項是消不掉的,尤其注意前幾個和最后幾個。比如這道題消掉中間項后的結果是這樣的:
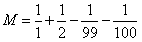
前面有兩個項,后面有兩個項是消不掉的。一定要注意!裂項相消法,在你裂出各項后,不要覺得馬上答案就水落石出了,就得意忘形忘乎所以。一定要注意前邊幾個和后邊幾個,哪些能消掉,哪些不能消掉,做好這些工作,才算是完整掌握裂項相消法。
Part.4
最后,我們引申到分式中來進一步理解裂項相消法,在分式中,也有裂項相消法的運用,例如:
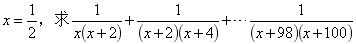
分母雖然不再是具體的兩個數字相乘,但仍然是符合我們的規律的。分母位置相乘的兩個數(在這里是式子)相差2,就提出二分之一:
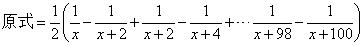
消掉中間項,得:
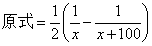
然后化簡代入或直接代入算出結果即可。
好了,這期的講解就到這里啦,對哪一塊不夠熟悉,想學習哪一方面的內容,歡迎在公眾號留言,我們下期再見哈!
最后,送大家一句成吉思汗的話:不要因路遠而躊躇,只要去,就必到達!祝各位研途順利!
同學們一定要自己重新歸納總結老師提到的重點哦,我們下期見!




